Converting Hexadecimal to Binary: A Comprehensive Guide and Converter

In the realm of digital information, hexadecimal (hex) and binary are two numerical systems that play a
crucial role in representing data at the fundamental level. Hexadecimal, with its base-16 system, is commonly used in computing and programming, while binary, with its base-2 system, is the fundamental
language of computers. Converting hexadecimal to binary is a fundamental skill for programmers and
anyone working in the field of information technology. In this comprehensive guide, we'll explore the principles behind hexadecimal and binary systems, understand the conversion process, and introduce a
handy converter for practical use.

Understanding Hexadecimal and Binary:

1. Hexadecimal System (Base-16):

Representation:

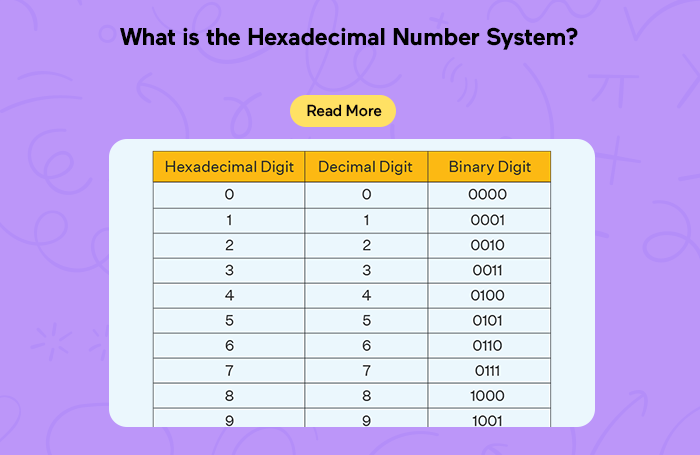
Hexadecimal uses 16 digits: 0-9 and A, where A represents 10, B is 11, and so on up to F, which is 15.

The base-16 system is a convenient way to represent large binary numbers compactly.

Example:

The hex number "1A" is equivalent to 1×161+10×160

, which is 26 in decimal or 00011010 in binary.

2. Binary System (Base-2):

Representation:

Binary uses only two digits, 0 and 1. It's the basic language of computers, where bits (binary digits) represent data.

Example:

The binary number "1011" is equivalent to 1×23+0×22+1×2

1+1×20

, which is 11 in decimal.

3. Converting Hexadecimal to Binary:

Converting a hexadecimal number to binary involves breaking down each hex digit and representing it in
binary.

Steps for Conversion:

1. Hex to Decimal:

Convert each hex digit to its decimal equivalent. Use the positional notation, where the rightmost digit is
multiplied by 160, the next digit 161, and so on.

Example: Hex "1A" becomes 1×161+10×160, which is 26.

2. Decimal to Binary:

Convert the obtained decimal number to binary.

Repeatedly divide the decimal number by 2, noting the remainder.

The binary equivalent is obtained by reading the remainder in reverse order.

Example: Decimal 26 becomes binary "11010."

3. Practical Converter:

For convenience, a practical Hexadecimal to Binary Converter simplifies the process. Here's how you can
use it:

4. Input Hexadecimal Number:

Enter the hexadecimal number you want to convert into the designated field.

5. Observe Binary Output:

The converter will instantly display the corresponding binary representation.

6. Copy or Utilize the Result:

Copy the binary output for use in your programming or computing tasks.

Benefits of Using a Hex to Binary Converter:

1. Efficiency:

The converter provides instant results, saving time and effort in manual calculations.

2. Accuracy:

Eliminates the possibility of human error in the conversion process.

3. Convenience:

Accessible online tools mean you can perform conversions anywhere with internet access.

Practical Applications:

1. Programming:

Programmers often work with hexadecimal and binary representations, especially when dealing with low-level programming and memory addresses.

2. Network Configuration:

In networking, hexadecimal and binary are used for configuring IP addresses and subnet masks.

3. Data Representation:

Understanding hexadecimal and binary is essential for interpreting and manipulating data at the binary
level.

4. Debugging:

In debugging processes, programmers may need to convert memory addresses or values between hexadecimal and binary.

Conclusion:

Converting hexadecimal to binary is a fundamental skill for anyone working in the fields of programming,
computer science, or information technology. Understanding the principles of these numerical systems
and having access to practical converters can streamline tasks and enhance accuracy in data representation.

As you navigate the intricacies of hexadecimal and binary, leverage online converters to simplify the
conversion process. Whether you're a seasoned programmer or a student delving into the world of
computing, mastering these numerical systems is a valuable asset in the digital landscape.